Wind power generates electricity by transferring energy from wind to mechanical energy. The principle behind wind turbines is very simple: the energy in the wind turns two or three blades around a rotor. The rotor is connected to the shaft, which spins a generator to create electricity. Wind turbines are mounted on a tower to capture the energy from the wind. The higher the blades are, the more they can catch faster and less turbulent wind. A simple wind turbine consists of three main parts, the blades, shaft, and generator, as shown in Figure 1.
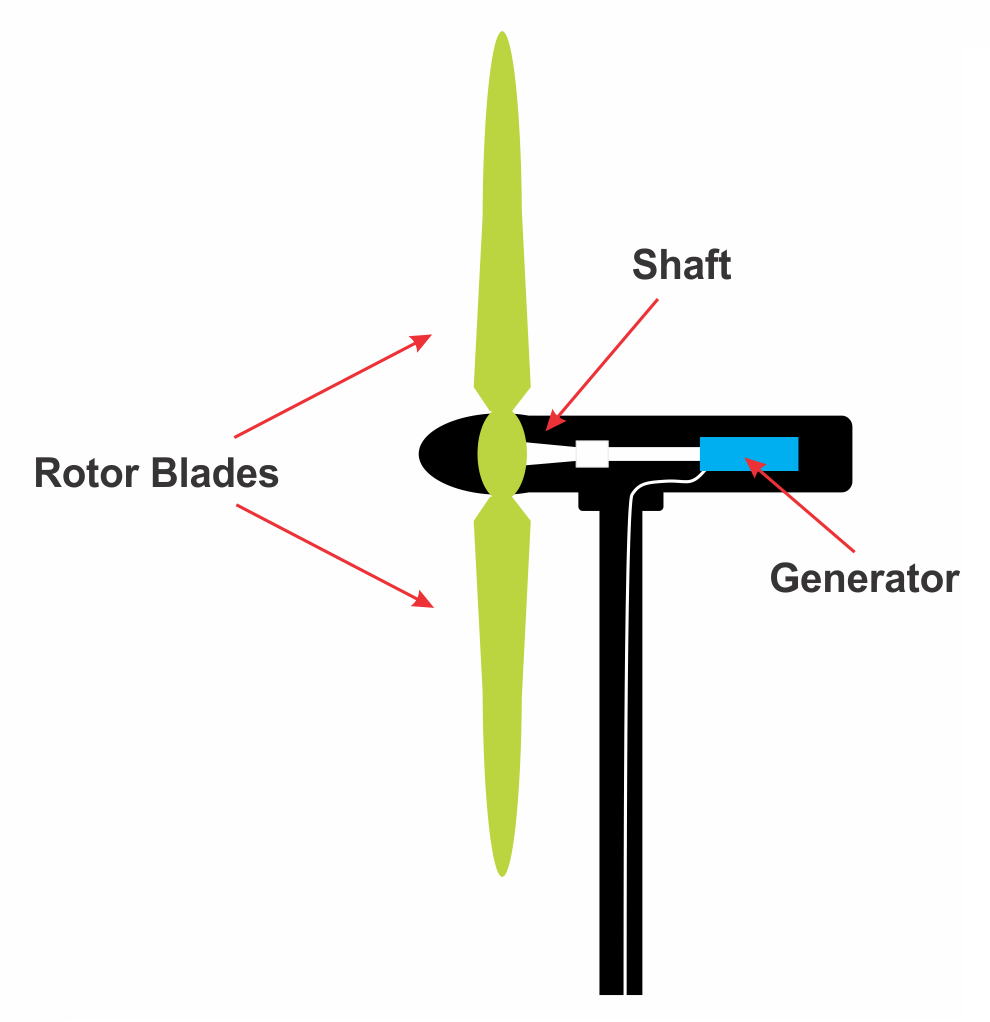
Figure 1. Major Parts of a Wind Turbine.
A simple description of these three parts is as follows:
1. Blades: The blade acts as a barrier to the wind. When the wind forces the blade to move, some of the wind energy is transferred to the rotor.
2. Shaft: When the rotor spins, the shaft also spins, which transfers the mechanical energy into rotational energy.
3. Generator: A generator uses the difference in electrical charge (electromagnetic induction) to produce a change in voltage.
Voltage is analogous to electrical pressure, which is the force that moves the electrical current. The voltage drives the electrical current (AC power) through the power lines for distribution. The electricity generated from a wind farm is usually fed into an electric power transmission network. The power produced by a wind turbine can be increased using a transformer so that it can be connected to the high voltage transmission system. Any surplus power can be sold back to the utility company.
Since the power in the wind is proportional to the cube of the wind speed, even small increases in wind speed can be significant. One method of obtaining higher wind speeds is to mount the turbine on a taller tower. In the first few hundred meters above the ground, the wind speed is affected by the friction that the air experiences as it moves across the earth’s surface. This friction is due to buildings, forests and other structures. Surfaces such as the ocean offer much less resistance to the wind.
When a force is transferred from one object to another, the second object will move in the same direction as the first. However, when a solid object transfers force or energy to a liquid, the reaction is different. Two forces are created called “drag” and “lift” (Figure 2). “Drag” and “lift” forces depend upon the shape of the object, velocities, direction of movement, and the density of the solid and fluid. In the case of wind turbines, the solid object is the blade, and the fluid is air.
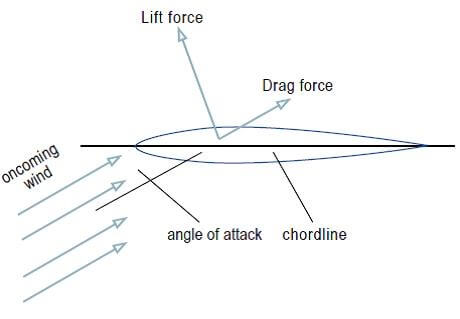
Figure 2. Lift and Drag Forces.
The amount of wind energy that can be captured and turned into electricity depends upon many factors, such as machine construction (rotor, generator, tower, and controls), terrain (topography, surface roughness, and obstructions) and the wind regime (velocity, timing, and predictability). A few simple calculations can help you to obtain a good energy estimate; however, more extensive wind turbine performance calculations are required to obtain a more accurate power production estimate. The power output of a wind turbine varies with wind speed, and every turbine manufacturer has a wind speed power curve. An example wind speed power curve is shown in Figure 3.
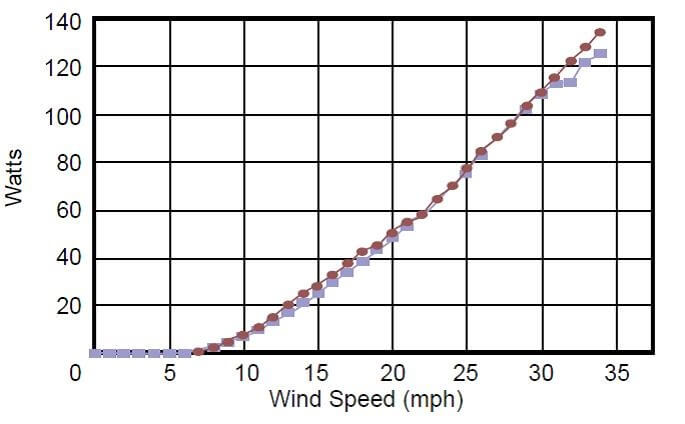
Figure 3. Example Wind Speed Power Curve.
A rough estimate of a wind farm’s annual energy production can be calculated using the sum of the wind turbine power ratings multiplied by the total hours in a year. The capacity factor (CF) is the ratio of the actual productivity in a year to the theoretical maximum, which is typically 20 - 40%. The number of megawatt-hours (MWh) can be calculated using the following equation:
# of MWh = CF × # hours × # days
For example, a 1-megawatt turbine with a capacity factor of 35% will not produce 8,760 megawatt-hours in a year (1 x 24 x 365), but only 0.35 x 24 x 365 = 3,066 MWh, with an average of 0.35 MW. There is data available for specific global locations, and this can be used to calculate the annual output.
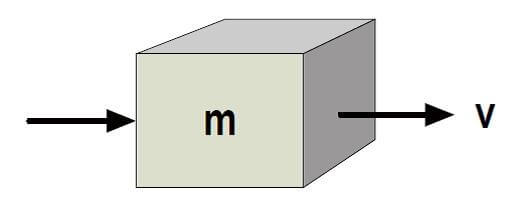
Figure 4. Mass of wind moving at a certain velocity.
If you have a mass, m, of air moving at speed, V, its kinetic energy (KE) can be expressed by a relationship illustrated in Figure 4:
Kinetic energy = ½ x m x V2
where m is the mass in kilograms, and V is the velocity in meters per second (m/s). By multiplying a volume of air by the density of air, ρ, (which is 1.2256 kg/m3), the mass of the air flowing through a volume per second can be expressed by:
Mass of air per second (m) = air density x volume of air flowing per second
The mass flow rate, m, through an area, A, is the product of air density, ρ, speed, V, and the cross-sectional area, A, can be expressed mathematically as:
Mass passing through A/Time = m = ρAV
Substituting for m in equation 2 above gives us an important relationship:
P = ½ x ρ x A x V3
where P is the power in the wind (watts), ρ is the air density (kg/m3) (at 15 °C and 1 atm, ρ = 1.225 kg/m3); A is the cross-sectional area through which the wind passes (m2); and V is the wind speed normal to A (m/s) (a useful conversion: 1 m/s = 2.237 miles per hour (mph)).
Since wind power increases with the cube of wind speed, doubling the wind increases the power by eightfold. Many wind turbines automatically turn themselves off at low-wind speeds. Equation 5 shows that wind power is proportional to the swept area of the turbine rotor and the blade diameter. Doubling the diameter increases the power available by a factor of four. The power obtained from a wind turbine is also related to the density of air. At higher elevations such as mountainous areas, the air density is lower. The densities in cold climates are also 10% higher than tropical regions. Consideration of these factors helps to explain the economies of scale with larger wind turbines.
Wind power harnesses the motion of the wind to provide kinetic energy. The three main parts of a wind turbine are the blades, shaft, and generator. The kinetic energy of the wind is captured by the turbine blades while moving. The moving of the blades spins a shaft, which leads to a generator. Wind power can be predicted using different methodologies, but estimates often consider tower height, air mass, wind speed, and rotor and blade dimensions. Utility-scale (megawatt-sized) power can be obtained from vast wind farms, or by integrating a wind turbine with an electrolyzer and fuel cell as part of a hybrid energy system. Wind energy is very advantageous for providing renewable energy, and it is targeted to be one of the largest contributors to providing energy in the future.

 Posted by
Posted by














Enter the code in the box below: