As we saw in the previous blog post, the process of ion exchange is influenced by a very large number of factors. The primary mode of ion transport is diffusion, which is process of the movement of atoms, ions, molecules, or energy from a region of high concentration to a region of low concentration. Diffusion will occur until the ion or molecule concentration becomes equal throughout the medium (solid, liquid, or gas). The ion exchange process, which occurs in ion exchange materials (IEMs) such as anion exchange membranes (AEMs) and cation exchange membranes (CEMs), can be broken down into the following steps (Figure 1):
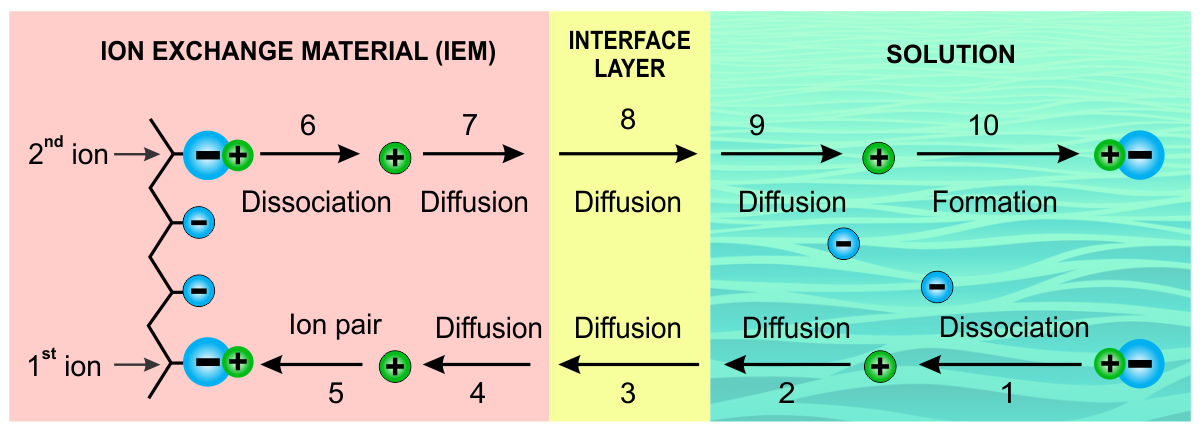
Figure 1. Steps in Ion Exchange Process.
(1) Step 1. The chemical molecule dissociates in the aqueous solution: This step occurs when ionic compounds are added to water. The individual ions interact with polar regions of the water molecules during the dissociation process, which disrupts their ionic bonds.
(2) Step 2. The ion diffuses from the solution to the interphase layer: This is a very thin interface layer that forms between the bulk forces that exist in the liquid and the ion change medium.
(3) Step 3. The ion diffuses through the interface boundary layer: The method of ion transport is solely due to diffusion.
(4) Step 4. The ion diffuses through the IEM: The ion travels into the IEM via diffusion.
(5) Step 5. The first ion associates with a functional group in the IEM: This association occurs due to the electroneutrality principle.
(6) Step 6. The second ion dissociates from the functional group on the IEM: This dissociation occurs because of the water in the IEM material and the electroneutrality principle.
(7) Step 7. The second ion diffuses from the bulk of the IEM to the surface: The movement of an ion may be due to a concentration gradient, electropotential, or a combination of factors.
(8) Steps 8 and 9. The second ion diffuses from the interface layer to bulk of the solution: Once the ion reaches the solution, the transport mechanism may change from diffusive to convective transport depending upon whether the solution is agitated.
(9) Step 10. The second ion associates with a molecule in the solution phase: The ion may associate with another oppositely charged ion in solution, depending upon the energy between molecules. This process is dynamic; therefore, some molecules will recompose themselves while others will stay in a dissociated state.
If we were fortunate enough to incorporate all of the variables involved with ion exchange into a model, we would have an unruly mathematical equation that would be too difficult to work with! Therefore, we will simplify the mathematical expressions by making certain assumptions. Most mathematical models only investigate the major contributors to the hypothesized phenomena and assume the other variables are constant or negligible. The most common approach to creating a kinetic model in ion exchange materials is to use conventional diffusion equations. However, we of course need to account for the actual ion exchange, which can complicate the model. The interactions associated with ion exchange are selectivity, electrocoupling, specific interactions, and changes in swelling. The diffusion processes in IEMs can be described by Fick’s first law:
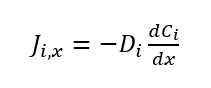
where Ji is the flux of the ion i in moles per unit time (in the x-direction), Di is the diffusion coefficient, Ci is the concentration in moles per unit volume. The diffusion flux (J) can describe the transport of the ions, water, or the transport of any species in the ion exchange membrane, surrounding medium, or any other layers involved. In very simple models, the diffusion coefficient is assumed to be a constant, which means that the flux is not subject to any other forces besides concentration inhomogeneity. For ion exchange, this is not the case due to electrocoupling of ionic fluxes. If D cannot be assumed to be constant, that means that variation needs to be taken into account. The Nernst–Planck equation can be used to take into account the influence of the electric field instead of equation (1):
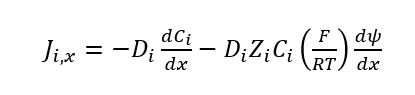
where ψ is the electric potential. If the two ions are in a medium with different concentrations, then their diffusion is affected by electrocoupling unequally. Fick’s law (equation 1) shows that the flux of diffusion only depends upon the concentration because there are no other forces acting on the molecular on the molecular level. However, if there is an unequal concentration of ion 1 and ion 2, the electrical field is a physical force acting on the ions, which produces a flux proportional to the concentration of each type of ion. Due to this phenomenon, the electric field affects the ion that has a higher concentration. If the concentration of one ion is small, then the second term in equation 2 is small, which means that it becomes more like equation 1. When two counterions are present, the two fluxes are coupled. The ion with the lowest concentration will be unaffected by the electric field and will primarily control the diffusion rate.
There are many ways to model the diffusion process, so if you look in the literature, you will see many forms of Fick’s diffusion equation. The science of thermodynamics looks at the diffusion process a little differently, and uses the gradient of chemical potential in the diffusion equation instead of the concentration gradient:
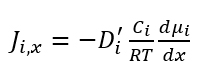
where µi is the chemical potential. The value for Di' can be empirically determined or calculated using different methods depending upon the system.
Every kinetic model makes assumptions to simply the model. The ion exchange material is not truly homogeneous, and this is especially the case if the ion exchange material is a polymer. Polymer IEMs can be cross-linked, gel-like, or porous. Most models assume a single quasi-homogenous phase like a solution. This assumption allows us to use equations 1 or 2. The diffusion coefficients in this type of system are sometimes assumed to be smaller than in an ordinary aqueous system due to a portion of the material volume being occupied by the polymer matrix material.
A popular type of IEM model is two-phase models that consider the polymer material as a solid network with interstitial pore space. In these models, it is assumed that diffusion only occurs in the pore phase; therefore, the diffusion is slower than with homogenous systems. This is because (1) a fraction of the pore cross-section not occupied by the polymer is available for diffusion, (2) the diffusion path is tortuous rather than straight, and (3) the mobility of the diffusing species may be reduced by interaction with the pore walls. These two-phase models are most appropriate for materials with a rigid, highly cross-linked matrix.
Conclusion
Simple models of the ion exchange process can be created using Fick’s law of diffusion, the Nernst-Planck equation, or a similar type of diffusive equation. Diffusion equations can be used to describe the ion mobility through the liquid and solid phases in ion exchange materials. The same equations can also be used to model liquid and gas molecules such as water and oxygen transport in the IEM. The type of model chosen depends upon the material, ions, and precision of the model outs desired by the scientist or engineer.

 Posted by
Posted by








