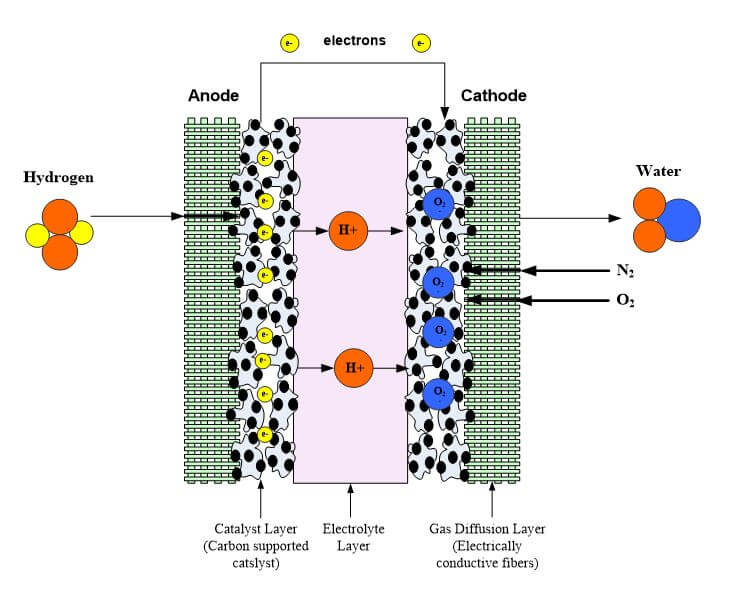
The fuel cell electrode layer is made up of the catalyst and porous gas diffusion layer. When the fuel in the flow channels meets the electrode layer, it diffuses into the porous electrode. The reactant travels to the catalyst layer where it is broken into protons and electrons. The electrons move to the external circuit to power the load, and the protons travel through the electrolyte until it reaches the other electrode to form water. Regardless of the fuel cell type, the catalyst layer must be very effective at breaking molecules into protons and electrons, have a high surface area and be preferably low-cost. It has been a challenge to find an inexpensive catalyst that is effective at breaking the hydrogen into protons and electrons.
Polymer electrolyte fuel cells have two catalyst layers where electrochemical reactions occur. At the anode, the hydrogen is broken into protons and electrons. The electrons travel to the carbon cloth, flow field plate, to the contact and then to the load. The protons move through the polymer exchange membrane to the cathode. At the cathode catalyst layer, oxygen comes from the air and combines with the protons to form water. The catalyst layers are often the thinnest in the fuel cell (5 – 30 microns) but are often the most complex due to multiple phases, porosity and electrochemical reactions.
Figure 1. Catalyst Transport Phenomena.
Figure 1 shows a schematic of the fuel cell catalyst layers where the chemical reactions occur at the two-phase interphase between the electrocatalyst and electrolyte. Scanning Electron Microscopy (SEM) shows an agglomerate-type structure where the electrocatalyst is supported on carbon agglomerate and covered by a thin layer of membrane. There have been many approaches taken to model the catalyst layer -- both microscopic and macroscopic models. Table 1 shows common methods and equations for modeling the catalyst layer.
| Model Characteristic | Description/equations |
| No. of dimensions | 1, 2, or 3 |
| Mode of operation | Dynamic or steady-state |
| Phases | Gas, liquid, or a combination of gas and liquid |
| Kinetics | Tafel-type expressions, Butler-Volmer equations, or complex kinetics equations |
| Mass transport | Nernst-Plank + Schologl, Nernst-Plank + drag coefficient, or Stefan-Maxwell equation |
| Ion transport | Ohm’s law |
| Membrane swelling | Empirical or thermodynamic models |
| Energy balance | Isothermal or full energy balance |
Table 1. Equations Used to Model the Catalyst Layer.
The fuel cell electrode is a thin, catalyst layer where electrochemical reactions take place. The electrodes are usually made of a porous mixture of carbon-supported platinum and ionomer. Catalyst particles must have contact with both protonic and electronic conductors to catalyze reactions. Furthermore, there must be passages for reactants to reach catalyst sites and for reaction products to exit. The contacting point of the reactants, catalyst, and the electrolyte is conventionally referred to as the three-phase interface. To achieve acceptable reaction rates, the effective area of active catalyst sites must be several times higher than the geometric area of the electrode. Therefore, the electrodes are made porous to form a three-dimensional network, in which the three-phase interfaces are located (Figure 1).
The catalyst surface area is a very important characteristic of the catalyst layer; thus, it is important to have small platinum particles (4 nm or smaller) with a large surface area finely dispersed on the surface of the catalyst support, which is typically carbon powders with a high mesoporous area (>75 m2/g). The typical support material is Vulcan XC72R, Black Pearls BP 2000, Ketjen Black International, or Chevron Shawinigan.
Catalyst layer models range from zero to three dimensions in the literature. Zero-dimensional models do not consider the actual structure of the catalyst layer. One-dimensional models account for the overall changes across the layer. There are also two and three-dimensional models that consist of the catalyst layer and the agglomerate. Agglomerate models can be either macro or micro models, depending upon how they are calculated.
The catalyst layer contains many phases: liquid, gas, different solids, and the membrane. Although various models have different equations, most of these are derived from the same governing equations, regardless of the effects being modeled. A Butler-Volmer type expression can describe the anode reaction in most cases except for those who use a fuel other than pure hydrogen. In these cases, the platinum catalyst becomes “poisoned.” The carbon monoxide adsorbs to the electrocatalytic sites and decreases the reaction rate. Some models account for this by using a carbon monoxide site balance and examining the reaction steps involved. For the cathode, a Tafel-type expression is commonly used due to the slow kinetics of the four-electron transfer reaction.
There are many more cathode than anode models in the literature. This is due to the slower reaction rate of the cathode due to water production and mass transfer effects. The anode can almost always be modeled as a simplified cathode model—except for the case when the hydrogen is not pure, and the poisoning of the electrocatalyst is included. The common types of models for the catalyst layer are presented in Table 2 and includes interface, microscopic, porous electrode, and agglomerate models.
| Type of Model | Description |
| Interface models | Interface models assume that the catalyst layers exist at the GDL/ membrane interface. The catalyst interface layer is the location where oxygen and hydrogen are consumed, and water is produced. |
| Microscopic and single-pore models | Microscopic and single-pore models contain cylindrical gas pores of a defined radius. The catalyst layer contains Teflon-coated pores for gas diffusion, and the rest of the electrode is flooded with liquid electrolyte. |
| Porous electrode models | Porous electrode models are based upon the overall reaction distribution in the catalyst layer. The agglomerates all have a uniform concentration and potential. |
| Agglomerate models | Agglomerate models assume a uniform reaction-rate distribution, and more accurately represent the actual structure of the catalyst layers. |
Table 2. Types of Models.
Many interface models assume that the catalyst layer only exists at the GDL/membrane interface. This assumption means that the catalyst layers are infinitely thin, and the structure can be ignored. There are several ways to accomplish this in a model. One method is to treat the catalyst layer as a location where hydrogen and oxygen are consumed, and water is produced. Models that focus exclusively on water management use this methodology with Faraday’s law for the mass balance between the membrane and diffusion medium. Faraday’s law is the rate at which hydrogen and oxygen are consumed, and water is generated, as shown in equations 1 - 3:
where N is the consumption rate (mol/s), I is the current (A), and F is Faraday’s constant (C/mol).
A more sophisticated method of modeling the catalyst layer is to use equations 1 - 3, and then use a polarization curve equation to produce a potential for the cell at a specific current density:
The Nernst equation is used to determine the theoretical electrical potential of the reaction. Equation 5 shows the potential for hydrogen electrochemically reacting with oxygen.
The Nernst equation is used to find the potential at the active locations, and the local potential using the half reactions. The equations for voltage losses can be incorporated with the Nernst equation to obtain a good approximation of the actual fuel cell potential.
Another commonly used approach for modeling the catalyst layers is to use the Butler-Volmer equation. The relationship between the current density and the activation losses for the anode is:
where ia is the transfer current density (A/m3), Vact is the activation electrode losses, io is the exchange current density, and αa is the anodic charge transfer coefficient. For the cathode:
The exchange current density depends on the local partial pressure of reactants and the local temperature. As the partial pressure of the reactants decreases, the exchange current density will also decrease -- which decreases performance. This illustrates how activation and diffusion limitations affect each other, and why the mass flux must be solved precisely. The exchange current density for the anode and cathode is:
where 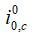
are the reference exchange current density, γ1 + γ2 is the reaction order, T0 is the reference temperature (303 K), and EA is the activation energy.
The early models of fuel cell catalyst layers that are microscopic, single-pore models. The catalyst layer typically comprises Teflon-coated pores for gas diffusion, with the rest of the electrode being flooded with liquid electrolyte. These models provide a little more detail about the microstructure of the catalyst layers than the interface models. There are two main types of single-pore models: gas pore and flooded agglomerate models. In the gas pore model, the pores are assumed to be straight, cylindrical gas pores of a certain radius. They extend the length of the catalyst layer, and reactions occur at the surface. The second type of model also uses gas pores, but the pores are filled with electrolyte and catalyst. In these pores, reaction, diffusion, and migration occur. The equations that were previously introduced (Equations 1 - 9) are primarily used in these models.
In the flooded agglomerate models, diffusion along with the use of equilibrium for the dissolved gas concentration in the electrolyte is used. The flooded agglomerate model shows better agreement with experimental data than the single pore model, which is expected because it models the actual microstructure better. A disadvantage of the single pore models is that they do not take into account the actual structure of the catalyst layer – which has multiple pores that are tortuous. However, the single pore models have helped to form some of the later, more complicated models that provide more realistic simulation results.
The porous electrode models calculate the overall reaction distribution in the catalyst layer without including the exact geometry details. The porous electrode models consider the agglomerate structure, but the layer has a uniform concentration and potential. This theory is concerned with the overall reaction distribution in the catalyst layer. Therefore, the main effects do not occur in the agglomerates, and the agglomerates have a uniform concentration and potential. The effect of concentration is accounted for in the calculation of the charge transfer resistance, which is from the kinetic expressions, and likely to be nonlinear. The charge transfer resistances should be in parallel with a capacitor, which represents double layer charging. This can be neglected for the steady state operation of the fuel cells and introduced if transients or impedance is studied. The governing equations for porous electrodes are shown in Table 3.
| Variable | Equation |
| Overall liquid water flux (NL) | Mass balance |
| Overall membrane water flux (NW) | Mass balance |
| Gas phase component flux (NG,i) | Mass balance |
| Gas phase component partial pressure (pG,i) | Stefan-Maxwell |
| Liquid pressure (PL) | Darcy’s Law |
| Membrane water chemical potential (uw) | Schlogl’s equation |
| Electronic phase current density (i1) | Ohm’s law |
| Membrane current density (i2) | Ohm’s law |
| Electronic phase potential (Φ1) | Charge balance |
| Membrane potential (Φ2) | Charge balance |
| Temperature (T) | Energy balance |
| Total gas pressure (pG) | Darcy’s Law |
| Liquid saturation (S) | Saturation relation/td> |
Table 3. Fuel Cell Catalyst Layer Variables.
The next level of models treats the catalyst layers using a complete simple porous electrode modeling approach. Therefore, the catalyst layers have a finite thickness, and all variables are determined as in Table 3. Some of these models assume that the gas phase reactant concentration is uniform in the catalyst layers; most allow the diffusion to occur in the gas phase.
Agglomerate models only consider effects that occur on the agglomerate scale. They assume a uniform reaction rate distribution. These models more accurately represent the structure of the catalyst layers than the simple porous electrode models. These are similar to the microscopic models, except the geometric arrangement is averaged, and each phase exists in each control volume. The characteristic length scale of the agglomerate is assumed to be the same size and shape. In the model, the reactant or product diffuses through the electrolyte film surrounding the particle and agglomerate where it diffuses and reacts. The equations again are similar to those listed in Table 3, except that either spherical or cylindrical coordinates are used for the gradients.
Modeling the catalyst layer is very complex because it has properties of all of the other fuel cell layers combined. Some of the important phenomena that need to be included in a rigorous catalyst layer model include mass, energy and charge balances along with a relation that accounts for the contact between the porous GDL and polymer membrane layer. Also, knowing how the catalyst agglomerates are distributed along the GDL is a challenge. The kinetics equations are the most important when modeling the catalyst layer. Commonly used equations are Fick’s law, Tafel equations, and the Butler-Volmer equation. There are many choices for how the catalyst layer is modeled, but the complexity of the model needs to be determined by the level of accuracy required and the resources available to help create the model.

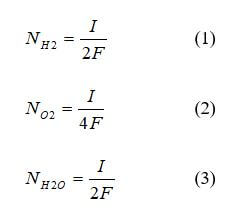
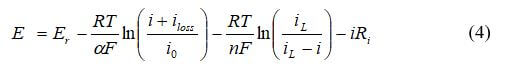
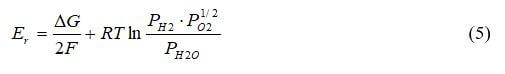
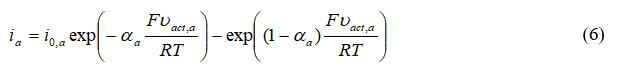
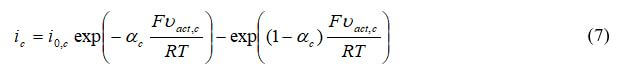
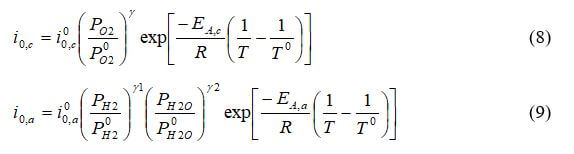
 Posted by
Posted by


















Enter the code in the box below: