The gas diffusion layer (GDL) in a fuel cell can consist of a single layer or a double layer (gas diffusion layer and a microporous layer). The GDL is an essential part of the fuel cell because it causes the gases to spread out to maximize the contact surface area with the catalyst layer. The thicknesses of various gas diffusion materials vary between 0.0017 and 0.04 cm with a porosity between 70% and 80%. The most commonly used GDL materials are carbon cloth and carbon paper. Properties of some of the commercially available carbon papers are shown in Table 1.
| Carbon Paper | Thickness (mm) | Porosity (%) | Density (g/cm3) |
| Toray TGPH 090 | 0.30 | 77 | 0.45 |
| Kureha E-725 | 0.35 | 60 - 80 | 0.35 - 0.40 |
| Spectracarb 2050A-1041 | 0.25 | 60 - 90 | 0.40 |
Table 1. Properties of Commercially Available Carbon Papers Used as Substrates for PEM Fuel Cell Electrodes.
The GDL manages the water in PEM fuel cells by only allowing a certain amount of water to contact the membrane/electrode assembly to keep the membrane humidified. Also, the GDL promotes the exit of liquid water from the cathode to help eliminate flooding. This layer is typically wet-proofed to ensure the pores in the carbon cloth or paper do not become clogged with water. A pictorial illustration of the GDL is shown in Figure 1.
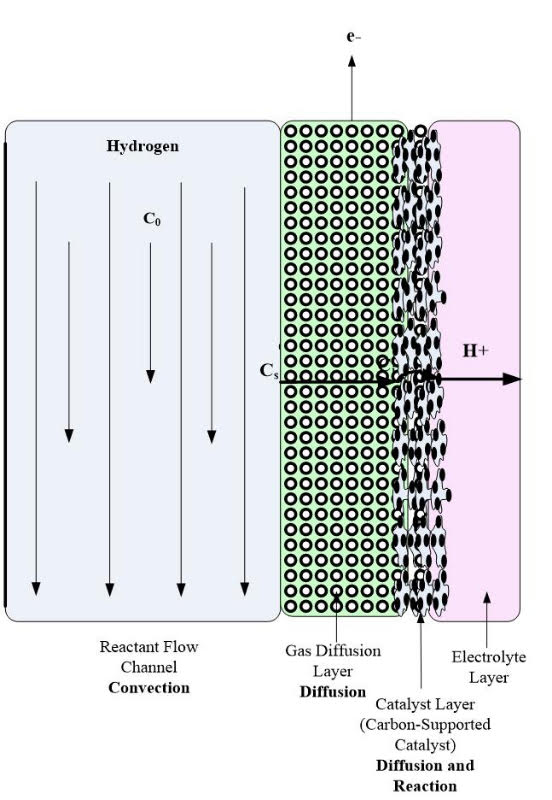
Figure 1. Pictorial Illustration of the GDL.
Many treatments exist for the gas diffusion layer. Most of these treatments are used to make the diffusion media hydrophobic to avoid flooding in the fuel cell. Either the anode or the cathode diffusion media, or both, can be PTFE treated. The diffusion material is dipped into a 5% to 30% PTFE solution, followed by drying and sintering. The interface with the catalyst layer can be fitted with a coating or microporous layer to ensure better electrical contacts and efficient water transport in and out of the diffusion layer. This layer consists of carbon or graphite particles mixed with PTFE binder. The resulting pores are between 0.1 and 0.5 microns (um) and are, therefore, much smaller than the pore size of the carbon fiber papers.
Mathematical models are beneficial for determining and predicting phenomena that you cannot see or measure; this is the case for the internal processes that occur in a fuel cell. Modeling the GDL is essential in determining the amount of reactant that reaches the catalyst layer, which in turn determines the amount of electricity that is being produced by the fuel cell. There are many different models in the literature for porous media, but the two main methods are: (1) the motion of gas molecules through the pores of the media; and (2) the interaction of the molecules of gas and solid. If the GDL has large pores, it is intuitive to think of the fraction of the media available for gas transport. Conversely, when the pore size in the substrate is very fine, and the size of the gas molecules and solid particles become comparable, the second option is used. These two options comprise the two schools of modeling porous media. We will introduce some of the characteristics of the GDL and the concepts needed to understand the basics of modeling of porous media.
A porous medium generally consists of solid matrix (material) and pore space. The description of the microscopic structure of pore space is difficult due to its geometrical complexity. There is typically an extensive network of pores communicating through relatively narrow constrictions. Since the shape of an actual pore is quite irregular, approximations of pore shape with regular geometries, such as a sphere, are commonly made in theoretical studies to study the effect of pore structure. After the geometry of the pore structure has been specified, surface areas and volumes of the pores can be calculated.
The void space in the porous medium is assumed to be filled with the different phases. The volume fraction occupied by each phase is the saturation of that phase. Therefore, the total fraction of all phases is one. In many models, two phases are usually considered: the liquid (l) and gaseous (g) phase. Each phase contains one or more components. The essential characteristics used to describe the phases are the mass fraction, density, and viscosity of each constituent. For example, there is usually hydrogen, oxygen, and water in the fuel cell. When performing these calculations, the amount of nitrogen (in air) and the humidity of the gases should also be included.
Another valuable property is capillary pressure, which is defined as the pressure difference between two immiscible fluids at equilibrium within the pore space, which can be expressed as:
where PG is the pressure of the gas phase, and PL is the pressure of the liquid phase. Capillary pressure involves the interfacial tension and the interfacial curvature. The method for calculating capillary pressure depends upon the pore shape. In a cylindrical capillary tube, capillary pressure is given by:
where 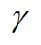
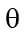
The (absolute) permeability is a measure of the material’s ability to transmit a single fluid at specified conditions. Since the orientation and interconnection of the pores are essential for flow, the permeability is not necessarily proportional to the porosity, but permeability (K) usually is strongly correlated to pore void fraction (φ).
In macroscale modeling, it is assumed that all phases may be present at the same location --although the phases do not mix. The permeability of one phase depends upon the saturation conditions and interaction with the substrate at a specific location.
The sum of the relative permeabilities at a specific location (with a specific composition) is not necessarily equal to one because they are nonlinear functions of the saturations. Relative permeabilities can depend on the pore-size distribution, the fluid viscosity, and the interfacial forces between the fluids.
There are several mechanisms by which gases and liquids can travel in porous media. This is known as “mass transport,” and can depend upon the molecule acceleration and environment. The molecules are grouped into distinct categories to help facilitate physical understanding and modeling. The four main types of transport are:
1. Free Molecule or Knudsen Flow, which occurs when the length between molecules is very small, or the species density is low,
2. Ordinary (Molecular) Diffusion, occurs when different species of a mixture move relative to each other under the influence of concentration, temperature, or other external force gradients,
3. Viscous Flow (Bulk/Continuum Flow), where the gas acts as a continuum fluid driven by a pressure gradient, and collisions between molecules dominate over collisions between the molecules and the wall, and
4. Surface Diffusion, where the molecules move along a solid surface in an adsorbed layer.
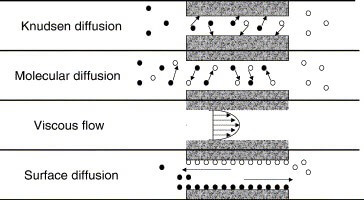
Figure 2. Illustration of Different Flow Types.
The appropriate transport mechanism can be used to predict the flow, or more than one transport mechanism can be combined into a model to provide more accurate results.
If the mean-free path of a molecule is less than 0.01 times the pore radius, ordinary diffusion is the primary mode of mass transport. If the mean-free path is greater than ten times the pore radius, Knudsen diffusion dominates. This means that Knudsen diffusion should be considered if the pore radius is less than about 0.5 μm. The typical gas diffusion layer has pores between 0.5 and 20 μm in radius, and a microporous layer contains pores between S0.05 and 2. Therefore, depending upon the material used, Knudsen diffusion may not have to be considered in gas diffusion layers, but it should be accounted for in microporous and catalyst layers.
Knudsen or free-molecule flow is where gas molecules collide more with each other than with the walls of the container. Knudsen flow occurs when the mean free path of the gas molecules is approximately the length scale of the container, or there are very low gas densities, (which means large mean free paths). In free molecule flow, there is no distinction between flow and diffusion (which are molecular phenomena). Also, gas composition is not important since there is no interaction between gas molecules of the same or different species.
Ordinary diffusion is the most common diffusion mechanism. For binary mixtures, the diffusive flux is directly proportional to its concentration gradient. In multicomponent mixtures, the fluxes of all the species should be considered since it affects the diffusive transport of any one species. This is because the momentum transferred to any one species will depend on the relative motion of all other species. The flux of a single species can be calculated in terms of the concentration gradients of the other species using Fick’s law of diffusion:
where J is the diffusive flux, D is the diffusion coefficient for each species, and n is the mole fraction of each species. For multicomponent mixtures, an expanded form of this equation, called the Stefan-Maxwell equation can be used.
Viscous (Darcy) flow refers to flow in the laminar continuum regimen that is caused by a pressure gradient. The gas behavior is determined by the coefficient of viscosity, which is independent of pressure for gases. Since bulk flow does not separate the components of gas mixtures -- mixtures of different gasses can be treated in the same manner as a pure gas. Under laminar flow conditions, the single-phase flow of incompressible fluids in porous media is governed by Darcy’s law:
where V is the Darcy velocity, K is the absolute permeability, is the dynamic viscosity of the fluid, ▽P is the pressure gradient, and p is the fluid density.
The gas diffusion layer must be a good conductor, chemically stable and able to withstand the temperatures and compression forces of the fuel cell stack. Many methods that have been used to model the GDL. Some of the conventional methods include modeling the gas and fluid through the pores or modeling the interaction of the gas/fluid with the solid porous media. Commonly used methods include Fick’s Law, Darcy’s Law, and the Stefan-Maxwell diffusion for the mass transport.

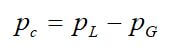
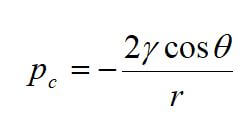
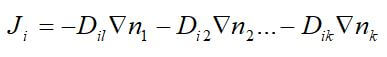
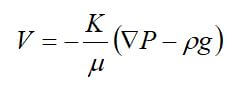
 Posted by
Posted by





















Enter the code in the box below: