There has been a lot of emphasis on the development of long-lasting, efficient and portable, power sources for further technology improvement in commercial electronics devices, medical diagnostic equipment, mobile communication and military applications. These systems all require the power source to be lightweight, energy efficient, and able to operate for long periods of time without refueling. Today’s popular power systems consist of disposable alkaline, zinc-carbon, or lithium sulfur-dioxide batteries, or rechargeable lead-acid, nickel-cadmium, or lithium-ion batteries. Current small devices such as cell phones and laptops use batteries that are heavy, costly, and have to be recharged or thrown out frequently. In addition, technological improvements in commercial electronics are slowing down because of the lack of small, high energy power sources to sustain the new features for long periods of time. Reducing the size of the fuel cell and increasing the performance allows technologies to become more advanced due to having more room in the device for electronics.
The military has a unique need to power portable devices that are currently powered by batteries. Devices are currently being developed for a soldier’s helmet, radio in the soldier's helmet, the computer around his waist, the weapon sight in his rifle, the night vision system, etc. All of these devices have batteries, which adds weight to the soldier, reducing his mobility and agility. This increases the soldier's agility, endurance, and survivability. Size is also important. Reducing the size of the fuel cell allows the soldier to carry more items in his pack. Today’s soldier is burdened by 16 different batteries, weighing approximately 2.5 each. The goal for the future soldier is to have a maximum of 4 batteries with less than 2.0 lbs in weight while maintaining >1 kW of power on a 72-hour mission. The current options are not viable for portable applications because they are heavy, impractical, and will not meet the current power requirements.
Fuel cells are known for high energy density, a variety of fuel sources, and ease of scaling for application-specific requirements. Fuel cells with polymer electrolyte membranes have been historically attractive because of their low-temperature operation and relatively simple construction. With the increase in attention towards MEMS technologies, investigation began on miniaturizing fuel cells during the late 1990s. Most of the work to date has consisted of miniaturizing the existing larger technologies without taking advantage of MEMS micro fabrication and processing techniques, or the advantages of fluid flow at the micro scale. There have been some experiments conducted using silicon wafers, photolithography techniques, etc, but without much forethought on what the optimal designs could be for micro scale fuel cells. This post reviews the work that has been conducted on micro fuel cells and describes relevant mathematical models in the literature.
Conventional polymer electrolyte membrane (PEM) fuel cells consist of two catalyst electrodes (the anode and cathode) separated by polymer electrolyte. Gaseous fuels are fed continuously to the anode (negative electrode), while an oxidant (oxygen from the air) is fed continuously to the cathode (positive electrode). Electrochemical reactions take place at the electrodes to produce an electric current. A schematic representation of a direct methanol fuel cell (DMFC), which is a type of PEM fuel cell, is shown in Figure 1.
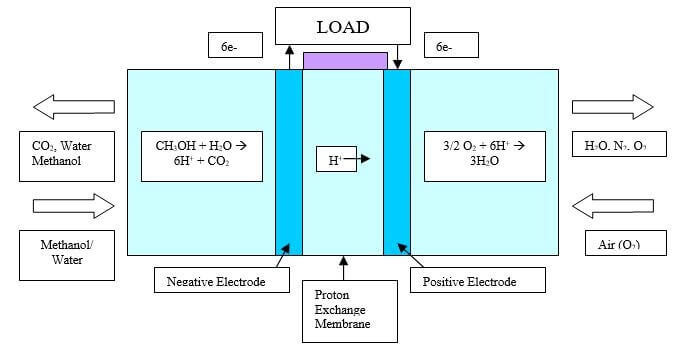
Figure 1. Direct Methanol Liquid-Feed Fuel Cell (DMFC)
The PEM fuel cell stack is historically made up of repeating cells separated by bipolar plates. Increasing the number of cells in the stack increases the voltage, while increasing the surface area of the cells increases the current. Figure 2 shows a representation of a traditional fuel cell stack.
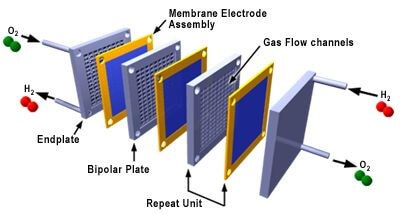
Figure 2. An Exploded View of a Polymer Electrolyte Membrane Fuel Cell Stack. (Picture:3M1)
The DMFC was developed to tackle the fuel storage problems of hydrogen, and to eliminate the need of a reformer to convert methanol to hydrogen for a hydrogen fuel cell to work. The DMFC is classified as a Proton Exchange Membrane Fuel Cell (PEMFC) because it also uses a PEM membrane. However, in addition to platinum, other catalysts like ruthenium (Ru) must be added to break the methanol bond in the anodic reaction.
The major obstacles for direct methanol fuel cells are: (1) drying out of the membrane (especially at high temperatures), (2) methanol crossover from the anode to the cathode across the membrane separator, (3) depolarization losses at the cathode due to methanol crossover, (4) efficient method of distributing the methanol and air on a micro-scale, (5) high costs of fuel cell stack materials and (6) systems design. All of these issues are present in MEMs-based fuel cells (many to a lesser extent), but there is an additional need to decrease fuel cell thickness. Many micro fuel cells utilize the traditional proton exchange membrane (such as Nafion®) to date, but the size of the fuel cell is limited greatly by this factor.
Since DMFCs are a new technology compared to other fuel cells, a number of problems need to be addressed to make DMFC system a viable technology for commercial and military applications. DMFC’s must become more compact, lightweight, cost-efficient, and they need to meet the power demands of commercial and military applications. DMFCs will become more compact, lightweight, and cost-effective when new materials and processes are selected. The main components that need to be improved are the polymer membrane, the electrodes, the bipolar plates, and the methanol feed subsystem.
The proton-conducting membrane usually consists of a PTFE-based polymer backbone, to which sulfonic acid groups are attached (eg. Nafion 112, 115, 117). The acid molecules are fixed to the polymer and cannot leak out, but the protons are free to migrate through the membrane. The polymer membrane is typically 175 microns, but there are also many polymer membranes that are commercially available that have a thickness of less than 175 microns. Membranes that are 50 microns or less in thickness, are frequently used, but are slightly unstable (chemically), and have not been as efficient in conducting protons in the DMFC.
The integration of Nafion into micro fuel cells is difficult because it swells during operation, which makes it incompatible with Nafion. Microtechnologies and nanotechnologies make the fabrication of nanoporous membranes possible. There have been studies with various concepts for the proton exchange structure in micro fuel cells [3]:
1. Nanoporous membrane
2. Nanochannels in silicon
3. Liquid electrolyte confined in a microchannel network
These configurations eliminate the methanol crossover that occurs in traditional membranes, allow the fuel cell to be operated at higher temperatures, and are less costly for mass production.
The electrodes are usually made of a porous mixture of carbon supported platinum or platinum/ruthenium. To catalyze reactions, catalyst particles must have contact with the protonic and electric conductors. There also must be passages for reactants to reach catalyst sites and for reaction products to exit. The contacting point of the reactants, catalyst, and electrolyte is conventionally referred to as the three-phase interface. To achieve acceptable reaction rates, the effective area of active catalyst sites must be several times higher than the geometrical area of the electrode. Therefore, the electrodes are made porous to form a three-dimensional network, in which the three-phase interfaces are located.
The thickness of the electrodes in traditional fuel cells is typically 250 – 2000 angstroms with a catalyst loading between 0.2 and 0.5 mg/cm2. For microfuel cells, the typical platinum loading is from 5 – 60 nm in thickness. An adhesion layer is deposited before the catalyst layer, and it is typical 25-300 angstroms in thickness. The catalyst loading is a cost-prohibiting factor for the DMFC. The cost of the DMFC stack would be lowered if the amount of platinum is lowered, another (cheaper) element is to be combined with it, the platinum is replaced with another element, or the fuel cell stack is miniaturized to the point where the catalyst is not as cost-prohibitive.
The diffusion layer is made of electrically conductive porous materials such as carbon or Toray paper. The conductivity of the paper can be improved by filling it with electrically conductive powder such as carbon black. To help remove water from the pores of the carbon paper, the diffusion layer can be treated with PTFE. Some micro fuel cell developers forgo the diffusion layer altogether, and platinum is sputtered directly on the proton exchange structure.
In the fuel cell stack, the bipolar plates separate the reactant gases of adjacent cells, connect the cells electrically, and act as a support structure. The bipolar plates have reactant flow channels on both sides, forming the anode and cathode compartments of the unit cells on the opposing sides of the bipolar plate.
Flow channel geometry affects the reactant flow velocities, mass transfer, and fuel cell performance. Bipolar plate materials must have high conductivity and be impermeable to gases. The material should also be corrosion resistant and chemically inert due to the presence of reactant gases and catalyst.
Most traditional bipolar plates are made from stainless steel or graphite. Stainless steel plates are heavy components for a portable power system. Solid graphite plates are highly-conductive, chemically inert, and resistant to corrosion, but are expensive, brittle, and costly to manufacture. Flow channels are traditionally machined or electrochemically etched to the graphite or stainless-steel bipolar plate surfaces. These materials are not suitable for mass production and would not work for a MEMS-based fuel cell system due to an inability to work with these materials on a microscale level. Typical materials that have been used in MEMs fuel cells are silicon, carbon paper, and thin metal foils, and traditional microfabrication techniques are beginning to be used with MEMS fuel cell.
In PEM fuel cells, the flowfield should be designed to minimize pressure drop (reducing parasitic pump requirements), while providing adequate and evenly distributed mass transfer through the carbon diffusion layer to the catalyst surface for reaction. The three most popular channel configurations for traditional fuel cells are: 1) serpentine, 2) parallel, and 3) interdigitated flow. Some small-scale fuel cells do not use a flow field to distribute the hydrogen and/or air but rely on diffusion processes from the environment. Since the hydrogen reaction is not rate limiting, and water blockage in the humidified anode can occur, a serpentine arrangement is typically used for the anode in smaller PEM fuel cells.
Fuel cell performance improves as the channel gas flow velocity increases since the increased flow velocity enhances mass transport. When investigating the effect of fuel cell geometry, the following geometric parameters need to be considered: the flow channel pattern, the channel and rib shape and the diffusion layer thickness as well as many other factors. The velocity in the flow channel will increase as the feature size decreases. However, one drawback of the smaller feature size is the increased pressure drop in the flow channels.
The reactant flow for the interdigitated design is parallel to the electrode surface. Often the flow channels are not continuous from the plate inlet to the plate outlet. The flow channels are dead-ended, which allows the reactant flow is forced under pressure to go through the porous reactant layer to reach the flow channels connected to the stack manifold. This design can remove water effectively from the electrode structure which prevents flooding and enhances performance. The interdigitated flow field is good since the gas was forced into the active layer of the electrodes where forced convection avoids flooding and gas diffusion limitations.
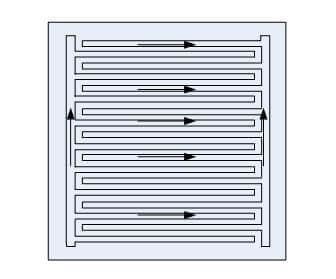
Figure 3: Interdigitated Flow Field Design
Scaling effects have been investigated for MEMS fuel cells [1] over feature sizes from 5 to 1000 microns. Flow velocities in the individual channels are inversely proportional to the feature size. Cell performance increases until the feature size is reduced to 500 microns, but the performance starts to decrease below this size. Cell performance begins to increase again when the feature size is 50 microns and below [1]. The pressure drop loss exceeds the increase of peak power in channels less than 50 microns.
The serpentine flow path is continuous from start to finish. An advantage of the serpentine flow path is that any obstruction in the path will not block all downstream activity of the obstruction. A disadvantage of serpentine flow is the fact that the reactant is depleted through the length of the channel, so that an adequate amount of the gas must be provided to avoid excessive polarization losses. When air is used as an oxidant, there are usually problems with the cathode gas flow distribution and the cell water management. When the fuel cell operated for long periods of time, the water formed at the cathode accumulates in the cathode. A force is required to move the water out of the channels. This design is relatively effective at providing flow distribution across the electrode surface of the fuel cell. However, this design may cause high pressure loss due to the relatively long flow path.
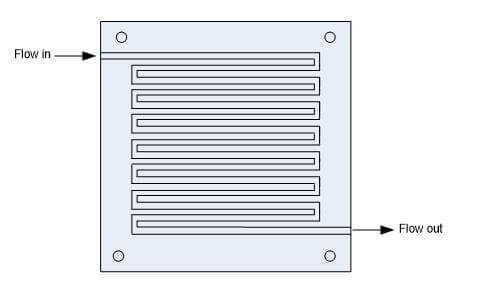
Figure 4: Serpentine Flow Field Design
In MEMS fuel cells, flow velocity is inversely proportional to the square of feature sizes. Serpentine channels may have the most pronounced scaling effect than other flow patterns. Better performance is gained between feature sizes of 483 – 99 microns, but the pressure losses under 200 microns is so large that it also negates the effect of down-scaling [1]. As in interdigitated channels, the increased performance in smaller channels is due to increased convection and reduced dead-zone. The pressure drop is high in serpentine channels because flow velocity scales with the square of the feature size, and the channel length is inversely proportional to the feature size. In [20], the serpentine flow field yielded a much higher than the parallel flow field, especially at high current densities. It is hypothesized that the higher Reynold’s number enhanced the mass transfer from the flow channel to the gas diffusion layer. When the channel depth was decreased from 1 mm to 300 microns, the power density performance increased by 71.9% [20]. When the channel depth was further reduced to 100 microns, the performance decreased by 8.6% [20].
A fuel cell stack has many cells stacked up so that the cathode of one cell is connected to the anode of the next cell. The main components of the fuel cell stack are the membrane electrode assemblies (MEAs), gaskets, bipolar plates with electrical connections and end plates. The stack is connected by bolts, rods or other method to clamp the cells together. The key aspects of fuel cell design:
• Uniform distribution of reactants to the cell
• Uniform distribution of reactants inside cell
• Maintenance of required temperature inside in each cell
• Minimum resistive losses
• No gas leakage
• Mechanical Sturdiness
The most common fuel cell configuration is shown in Figure 2. Each cell (MEA) is separated by a plate with flow fields on both sides to distribute the fuel and oxidant. The fuel cell stack end plates have only a single-sided flow field. Most fuel cell stacks, regardless of fuel cell type, size, and fuels used is of this configuration.
Most MEMS systems use silicon as the preferred material because of the availability, low-cost and various processing technologies available. Some of the processes normally used to create micro fuel cells are anisotropic etching, deep reactive ion etching (DRIE), deposition of various materials using CVD and PVD. Polymers are also beginning to be used, but silicon/glass systems are mechanically more stable, can resist high temperatures/pressures, and are basically chemically inert. However, silicon is brittle, and polymers allow configurations and alternative processing techniques. Some of the polymers that are being researched include PMMA and PDMS using ion etching, polymeric surface micromachining, hot embossing, soft lithography and laser machining. Stainless steel foil and copper films are also being researched as materials for fuel delivery/current collector plates [3].
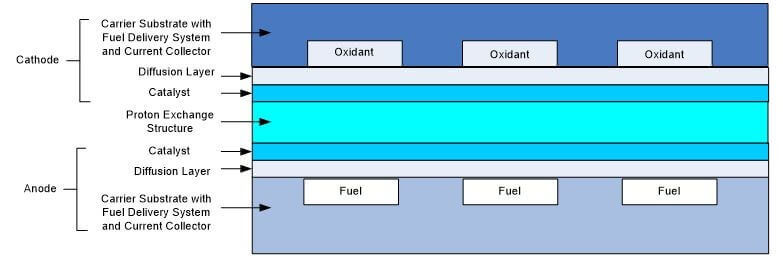
Figure 7. Basic Micro Fuel Cell Based Upon Traditional Fuel Cell Design
The necessary improvements for DMFC performance and operation demand better design, materials and optimization. These issues can only be addressed if realistic mathematical process models are available. There are many published models for PEM fuel cells, but only a small number for DMFCs. Table 1 shows a comparison of recent publications describing the key features of the mathematical models.
The first column of Table 1 shows the reference each mathematical model. The second column summarizes whether the model was dynamic or steady-state. The next seven columns present the dimensionality of the layers of the traditional DMFC. A “0” means that the parameter is described by a lumped parameter model, and a “1” means that the component was modeled 1-D. The next two columns of Table 1 present the type of electrode kinetic expression. In most of the 1D models, simple Tafel type expressions are used. Only a few papers use Butler-Volmer type expressions, and a few other models use more realistic, complex multi-step reaction kinetics for the electrochemical methanol oxidation method. The next two columns compare the phases used for the anode and cathode structures. It is well-known that there are 2 phases (liquid and gas) under a variety of operating conditions coexist. On the anode side, there is production of carbon dioxide in the catalyst layer, especially at elevated temperatures. Inside the cathode structure, water may condense, and block the way for fresh oxygen to reach the catalyst layer.
| Ref | Dyn/ss | A | AD | AC | M | CC | CD | C | Anode Kinetics | Cathode Kinetics | Anode Phase | Cathode Phase | Mass Transport (anode) | Mass Transport (membrane) | Mass Transport (cathode) | Membrane Swelling | Energy Balance |
| 44,45 | Dyn | 0 | 0 | 0 | 1 | 0 | - | - | Complex | BV | L | G | Eff.F | NP+S | - | - | Isothermal |
| 46 | SS | 0 | 0 | 1 | 0 | 1 | - | - | Tafel | Tafel | L | G | - | NP+dc | - | - | Isothermal |
| 47 | SS | 0 | 1 | 0 | 0 | 0 | - | - | Tafel | Tafel | G+L | G | Eff.F | NP+dc | - | - | Isothermal |
| 48 | SS | 0 | 1 | 0 | 0 | 0 | - | - | BV | BV | G+L | G | NP+S | NP+S | - | - | Isothermal |
| 49 | SS | 0 | 0 | 1 | 1 | - | - | - | Complex | - | L | G | NP | NP+dc | - | - | Isothermal |
| 50 | SS | 0 | 1 | 1 | 0 | - | - | - | Tafel | - | L | G | NP | NP+dc | - | - | Isothermal |
| 51 | SS | 0 | 1 | 1 | 1 | 1 | 1 | 0 | Complex | Tafel | G+L | G+L | NP(1), MS(g) | NP+irrev, TD | SD(1), MS(g) | Empiric | Isothermal |
| 52, 53, 54 | SS | - | 1 | 1 | 1 | 1 | 1 | - | Complex | Tafel | G+L | G | NP(1), MS(g) | MS | MS | TD Model | Isothermal |
| 55 | SS | 0 | 1 | 1 | 1 | 1 | 1 | 0 | Tafel | Tafel | G+L | G+L | NP | NP+S | NP(1), MS(g) | - | Isothermal |
| 56 | SS | 0 | 0 | 0 | 0 | 0 | 0 | 0 | Tafel | Tafel | G+L | G+L | Eff.F | - | Eff.F | - | Isothermal |
| 57 | SS | 1 | 1 | 1 | 1 | 1 | 1 | 1 | Tafel | Tafel | L | G | F | NP+dc | Eff.F | - | Isothermal |
| 58 | Dyn | 0 | 1 | 0 | 1 | 0 | 1 | 0 | BV | BV | L | G | MS | MS | MS | TD Model | Full Balance |
BV: Butler-Volmer, dc: drag coefficient; dyn: dynamic, eff:effective, F: Fick’s, G: gas, irrev: irreversible, L: liquid, MS: Maxwell-Stefan dynamic, NP: Nerst-Plank, S: Schlogl, SD: surface diffusion, SS: steady-state, TD: thermodynamics
DMFC Layers: A: Anode compartment/flow channels, AD = Anode Diffusion Layer, AC = anode catalyst layer, M = membrane/PEM, CC = cathode catalyst layer, CD = cathode diffusion layer, C = Cathode compartment/flow channels
** A “0” means that the parameter is described by a lumped parameter model, and a “1” means that the component was modeled 1-D.
An important feature of each model are the mass transport descriptions of the anode, cathode, and polymer exchange membrane. There are several mass transport models that are used. Simple Fick diffusion models (F) and effective Fick Diffusion (eff F) models typically use experimentally determined effective transport coefficients instead of Fick diffusivities and do not account for convective flow contributions. Therefore, many models use Nerst-Planck (NP) mass transport expressions that combine Fick’s diffusion with convective flow. The convective flow is typically calculated from Darcy’s Law using different formulations of the hydraulic permeability coefficient. Some models use Schlogl’s formulations (S) for convective flow instead of Darcy’s law, which also accounts for electro-osmotic flow, and can be used for mass transport inside the PEM. A very simple method of incorporating electro-osmotic flow in the membrane is by applying drag coefficient models (dc), which assumes a proportion of convective water and methanol flow to proton flow. Another popular type of mass transport description is the Maxwell-Stefan formulation for multi-component mixtures. This has been used for gas-phase transport, but this equation would be better used for liquid-vapor-phase mass transport. Only one recent model use this for both phases. Surface diffusion models and models derived from irreversible thermodynamics (irrev. TD) are seldomly used. Mass transport models that use effective transport coefficients and drag coefficients (F, eff F, NP, S) usually only yield good approximations to experimental data under a limited range of operating conditions.
The second last column of Table 1 presents whether the swelling of the PEM membrane is taken into consideration. Most models assume a fully hydrated PEM. In one case [51], the water uptake is described by an empirical correlation, and in [52 – 54] a thermodynamic (TD) model is used based upon the change of Gibbs free energy inside the PEM based upon water content. The last column notes whether the published model includes energy balances. Obviously, all models that assume an isothermal cell operation had no energy balances included.
Proton exchange membrane and direct methanol fuel cells are among the most promising fuel cell technologies to date. Direct Methanol Fuel Cells (DMFC) are predicted to be the choice power source for future portable applications. The low-cost of methanol, high energy density, and inherent safety explain the immense interest in this power source. One of the major technical challenges of the DMFC is the development of a mathematical model for a micro direct methanol fuel cell that will help to optimize, design and manufacture future micro fuel cells. MEMS fuel cells are a relatively new field where the larger stacks have mostly been miniaturized. The development of these micro DMFC models will lead to improved micro direct methanol fuel cells without the traditional membranes that may aid in bring micro fuel cell technology to fruition more quickly.

 View reference page
View reference page Posted by
Posted by
















