A numerical model was developed to predict the water concentration, temperature, potential and pressure across a Nafion membrane used in proton exchange membrane (PEM) based fuel cells. The numerical model consists of simultaneously calculating the diffusive flux for water and hydrogen, the proton potential and the pressure and temperature at each node.
Keywords: Proton exchange membrane fuel cell; Nafion membrane
In proton exchange membrane fuel cells (PEMFC), the fuel travels to the catalyst layer, and is decomposed into protons (H+) and electrons. The electrons travel to the external circuit to power the load, and the hydrogen protons travel through the electrolyte until they reach the cathode to combine with oxygen to form water. The electrolyte layer is essential for a fuel cell to work properly. The PEMFC electrolyte must provide high ionic conductivity, present an adequate barrier to the reactants, be chemically and mechanically stable, have low electronic conductivity, be easily manufactured and preferably low-cost.
The polymer electrolyte membrane contains water and hydrogen protons; therefore, the transfer of the water and protons transfer are important phenomena to investigate [1-10]. In addition to species transfer, the primary phenomena investigated inside the membrane are energy transfer and potential conservation [9]. For water transport, the principle driving forces modeled are a convective force, an osmotic force (i.e. diffusion), and an electric force [1-10]. The first of these results is from a pressure gradient, the second from a concentration gradient, and the third from the migration of protons from anode to cathode and their effect (drag) on the dipole water molecules. Proton transport is described as a protonic current and consists of this proton driven flux and a convective flux due to the pressure driven flow of water in the membrane [1-10]. Figure 1 illustrates the transport phenomena for the protons taking place within the membrane.
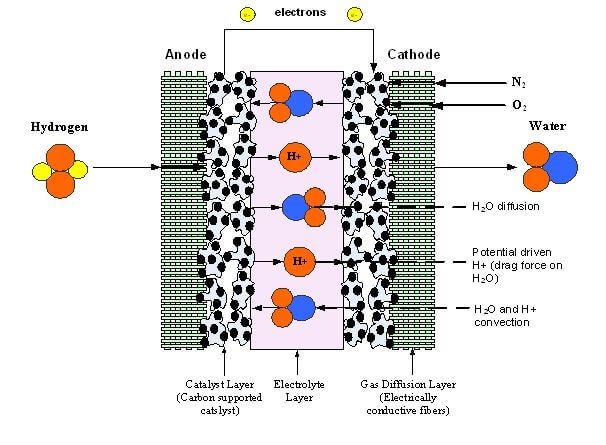
Figure 1. Membrane Transport Phenomena
Most membrane models in the literature are isothermal, and therefore, unsuitable for water and heat management studies. A relatively small number of models include non-isothermal effects [7, 12, 13, 15, 16], and typically, the ones that do focus on modeling multiple fuel cell layers, with simplifying assumptions for the membrane layer. Also, many models that do allow for operating temperature changes, but not a temperature gradient. For most conditions, the change in parameter values with temperature has a more significant impact than accounting for temperature gradients, although the two are coupled to a certain extent.
Transient models examine changes in potential and transport phenomena (flow rates, water production and current density). These models are aimed at examining different load requirement. Most models do not examine transients due to the computational cost and complexity. Some codes in the literature can take on the order of tens of minutes in certain circumstances [24]. One of the first models to examine transients in PEM fuel cells is a stack –level model by Amphlett et al. [20]. This is an empirical model that examines temperature and gas flow rates. There have been some more complex transient models that have examined the behavior of water content in the membrane that have demonstrated the effects of the membrane drying out [10, 21]. Other transient models have either not included liquid water, do not report transient results or focuses mainly on water transport in the gas diffusion layers [15, 16, 17, 18, 19, 20, 22]. There are no results reported in the literature that simultaneously show the temperature, potential, water concentration and pressure profile in the membrane based upon varying current densities, temperatures and pressure gradients.
The model presented in this paper is a compact model that can simultaneously calculate the temperature, pressure water concentration and potential at a user-specified number of positions through the membrane. Since the code uses built-in MATLAB functions, it is only a few hundred lines, can compute hundreds of points within the membrane within seconds, can easily be expanded to include additional transient boundary conditions and can be easily integrated into an overall fuel cell model.
Proton exchange membrane fuel cell (PEMFC) models are necessary to predict fuel cell performance to optimize performance to help reduce development costs and time. Water management is critical for efficient fuel cells due to its large effect on ohmic and mass-transport overpotentials, operating conditions and membrane electrode assembly design.
Since the membrane is the key element in a fuel cell, a lot of attention has been focused on it in terms of modeling. In the literature, there are both macroscopic and microscopic models. The microscopic models focus on single ions, and pore-level effects, and the macroscopic models are typically more empirical and focus on the transport phenomena. Although the microscopic models reveal valuable information about what occurs in the membrane, they are generally too complex to use in an overall fuel cell model. The membrane system is assumed to consist of three main components: the membrane, protons and water.
Proton exchange membrane fuel cell (PEMFC) models are necessary to predict fuel cell performance to optimize performance to help reduce development costs and time. Water management is critical for efficient fuel cells due to its large effect on ohmic and mass-transport overpotentials, operating conditions and membrane electrode assembly design.
Most models of the polymer exchange membrane are overly complicated. Many secondary effects are often included, such as convective (Darcy) water flow, membrane swelling and other membrane properties that are dependent upon water content. Simple models are desirable due to reduced model development time; reduce computational time, and easy integration into other models.
Current fuel cell modeling focuses on effects with specific designs and materials. Verbrugge and Hill [1] and Bernari and Verbrgge [2] developed a steady-state, isothermal, one-dimensional model for the electrochemical performance in a PEMFC. They claim that the liquid and gas pressure evolve separately in the GDL layer, which implies that they are not at equilibrium with each other. This model only applies to fully hydrated membranes, and the drag flux due on the water molecules is not considered.
Springer, Zawodzinski and Gottesfeld [3] presented a 1D, steady-state isothermal model of a PEMFC with emphasis on water transport phenomena through a Nafion membrane. An improved model with a detailed treatment of ion transport and ionic conductivity in the catalyst and backing layer was developed in [4]. This model predicted the mass transport limitations at high current densities. In [5], Springer, Zawodzinski, Wilson and Gottesfeld provide experimental and theoretical results for unsteady-state effects in a 1-D isothermal PEMFC stack. They use a frequency diagram to quantify the specific influences of several sources of losses such as activity in the cathode and conductivity of the catalyst layer and the membrane.
Weisbrod, Grot, and Vanderborgh [6] developed a through the electrode model to predict fuel cell performance as a function of water balance in the channels, and across the membrane. The model predicts the influence of both the catalyst layer thickness, and its Platinum catalyst loading.
Nyguyen and White [7] developed a 1-D, steady-state water and heat management model for PEMFCs. This model does not study the details of the membrane and the catalyst layers separately since it models that entire electrode as one unit. It does steady the affect of humidification levels and their effect on fuel cell performance. This model was enhanced in [8], with the addition of a linear model for the membrane, and then a 2-D, steady-state model for multispecies transport in the electrodes. This model studies the effect of an interdigitated gas distributor on PEMFC performance. However, it was unable to predict the effect of liquid water within the system. Thirumalai and White [9] used the model developed in [8] to predict the operating parameters, flow field design and gas manifold geometry on the performance of the fuel cell stack.
Van Bussel, Koene and Mallant [10] create a 2D dynamic model, with a 1D model through the membrane. The model is based upon the work of Springer et al. [3], but uses experimental data from Hinatsu, Mizhuta and Takenaka [11]. The model showed that current density can vary strongly along the gas channels, especially when operating with dry gases.
Gurau, Kakac, and Lui [12] developed a 2-D non-isothermal model. They considered the gas channel, and the diffuser-catalyst layer a single entity. The model shows a non-uniform, reactant distribution has an important impact on the current density distribution. This model is based upon an infinitely thin catalyst layer, which is unable to predict the voltage due to transport limitations in the catalyst layer.
Fuller and Newmann [13] and Weber and Newmann [14] developed a steady-state, 2-D model for the membrane electrode assembly. Unlike other models, concentration solution theory was used. They argued that water was produced in the gaseous phase at the catalyst surfaces. Their model is valid if there is no condensation within the catalyst layer.
The remainder of this paper is organized as follows: In Section 2, the proposed model is derived from the basic cell parameters. Section 3 details the numerical implementation of the model, while Section 4 presents the results and the associated discussions. The conclusions are drawn in Section 5.
Figure 1 shows a membrane with water and proton flow in the region 0 < y < N. As in all earlier papers on transport phenomena in the membrane, the hydrogen protons are constant. Conservation equations are required for the water, protons, energy and potential.
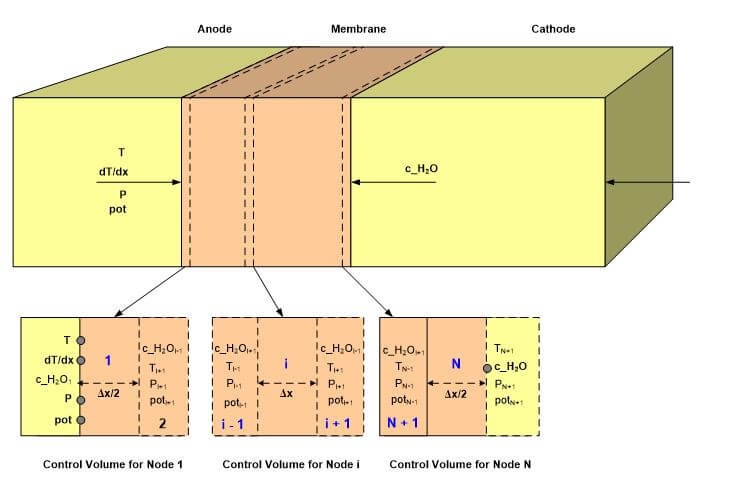
Figure 2 Slices created for 1-D membrane model
The main assumptions include the following: rate limiting water diffusion in the Nafion membrane, steady state, water diffusion perpendicular to the membrane surface (membrane thickness is much smaller than the channel length), constant pressure along the channels, constant concentration in the gas stream at any given location along the channel (plug flow behavior), constant temperature, ideal gas behavior, negligible gas diffusion through the membrane, negligible pressure drop across the membrane (no permeation through the membrane), membrane properties independent of water content (diffusion coefficient and membrane thickness), equilibrium between channel and membrane interfaces, and linear relationship between membrane water content and channel water concentration (analogous to Henry's law).
Click the link below to access the full article for viewing or to download for free.

 View or download article
View or download article Posted by
Posted by













Enter the code in the box below: