 Thermodynamics is the study of energy changing from one form to another. Many predictions can be made using thermodynamic equations, and these are essential for understanding fuel cell and electrolyzer performance because these devices transform chemical energy into electrical energy or vice versa. Studying these concepts allows a scientist or engineer to predict states of the fuel cell system, such as voltage, temperature, pressure, and amounts of hydrogen, oxygen, water in an electrolyzer or fuel cell system. Some concepts need to be defined to understand thermodynamic analysis, such as absolute enthalpy, specific heat, entropy and Gibbs free energy. The definitions are as follows:
Thermodynamics is the study of energy changing from one form to another. Many predictions can be made using thermodynamic equations, and these are essential for understanding fuel cell and electrolyzer performance because these devices transform chemical energy into electrical energy or vice versa. Studying these concepts allows a scientist or engineer to predict states of the fuel cell system, such as voltage, temperature, pressure, and amounts of hydrogen, oxygen, water in an electrolyzer or fuel cell system. Some concepts need to be defined to understand thermodynamic analysis, such as absolute enthalpy, specific heat, entropy and Gibbs free energy. The definitions are as follows:
1. Absolute enthalpy and enthalpy: Absolute enthalpy includes both chemical and sensible thermal energy. Chemical energy or the enthalpy of formation (hf) is associated with the energy of the chemical bonds, and sensible thermal energy (Δhs) is the enthalpy difference between the given and reference state. When analyzing thermodynamic systems, the sum of the internal energy (U) and the product of pressure (P) and volume (V) appears so frequently that it has been termed “enthalpy” (H), and is denoted as: H = U + pV. The values for the internal energy and enthalpy can be obtained from thermodynamic tables when the temperature and pressure are known.
2. Specific heat: Another property that is important in the study of fuel cells and electrolyzers are the specific heats – which are useful when using the ideal gas model. Specific heat is a measure of the amount of heat energy required to increase the temperature of a substance by 1 ºC (or another temperature interval). The specific heat is available in many thermodynamic property tables. The specific heat and similar quantities are all very usual in thermodynamics and energy balances because they relate the temperature change of a system to the amount of energy added by heat transfer.
3. Entropy: Entropy is another important concept, which can be loosely defined as the amount of “disorder” in a system. It is a measure of the quantity of heat that shows the possibility of conversion into work.
4. Gibbs free energy: Gibbs free energy is the amount of useful work that can be obtained from an isothermal, isobaric system when the system changes from one set of steady-state conditions to another.
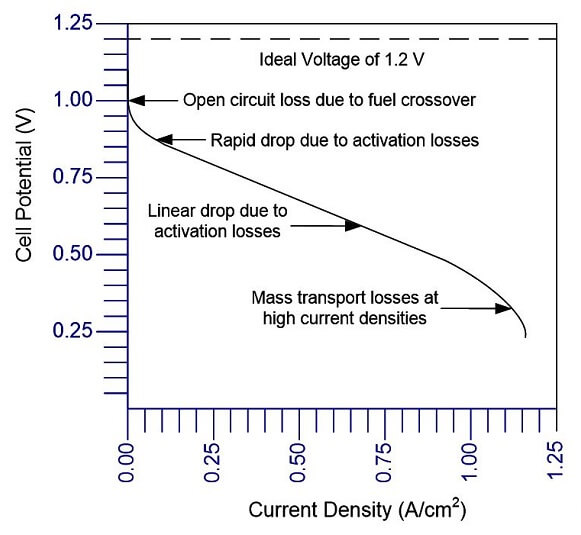
In addition to calculating energy quantities, when the conversion from chemical energy into electrical energy or vice versa creates electron flow through the materials in the fuel cell or electrolyzer. The single fuel cell or electrolyzer cell provides a voltage dependent on operating conditions such as temperature, applied load, and fuel/oxidant flow rates. The standard measure of performance is the polarization curve, which represents the cell voltage behavior against operating current density. Depending upon how the curvature of the polarization curve, you can obtain an idea of why where in the fuel cell the voltage is being lost. The maximum fuel cell performance is then examined through the ideal (reversible) voltage of the system, which is calculated using thermodynamics, and the net (actual) output voltage of the system.
Net output voltage: The reversible cell potential minus the irreversible potential at a certain current density. The irreversible potential is the actual voltage. The net output voltage can be expressed mathematically as: V = Vrev - Virrev, where Vrev = Er is the maximum (reversible) voltage of the fuel cell, and Virrev is the irreversible voltage loss (overpotential) occurring in the cell.
Figure 1. Hydrogen–oxygen polarization curve at equilibrium.
The actual voltage is lower than the theoretical model due to reaction, charge and mass transfer losses. As shown in Figure 1, the performance of an electrolyzer or fuel cell can be illustrated using a polarization curve that can be broken into three sections: (1) activation losses, (2) ohmic losses, and (3) mass transport losses. Therefore, the operating voltage of the cell can be represented as the departure from ideal voltage caused by these three losses (polarizations): V = Er + Vact + Vohmic + Vconc, where V is the cell potential, E is the thermodynamic potential or Nernst voltage, Vact is the voltage loss due to activation polarization, Vohmic is the voltage loss due to ohmic polarization and Vconc is the voltage losses due to concentration polarization.
The explanation of the terms in Equation 3 and Figure 1 stems from the detailed study of different disciplines. The Nernst (ideal thermodynamic) voltage comes from the study of thermodynamics, activation losses are described by electrochemistry, charge transport examines ohmic losses and concentration losses can be explained by mass transport. These subjects are often studied in advanced college programs such as chemistry, physics, chemical or mechanical engineering. The Nernst (ideal thermodynamic) voltage is calculated using thermodynamics and is the ideal (theoretical) system voltage. Activation losses mainly occur when the electrochemical reactions are slow to produce current. As the PEM fuel cell produces more current, the activation losses increase at a slower rate than the ohmic losses.
Ohmic losses are due to electrons not transferring between materials and terminals. Charges move from the electrode where they are produced to the load where they are consumed. The two major types of charged particles are electrons and ions, and both electronic and ionic losses occur in the fuel cell. The electronic loss between the bipolar, cooling and contact plates are due to the degree of contact that the plates make with each other. The ionic charge losses occur in the fuel cell membrane when H+ ions travel through the electrolyte.
Concentration losses are due to the reactant (gases or water) not adequately arriving at the electro-catalytic sites for the reaction to occur, which can significantly affect device performance. These mass transport losses can be minimized by making sure that the right amount of hydrogen, air and water travel through the flow field plates, gas diffusion layer and catalyst layers.
Thermodynamics provides the theoretical limits and many of the necessary equations for predicting fuel cell and electrolyzer performance. Some of these concepts include the theoretical fuel cell potential and net output voltage. It also provides the basis for evaluating the properties of these systems, especially the pressure and temperature effects on the cells.

 Posted by
Posted by


















Enter the code in the box below: